當需要在某一陣列中，求某一段區間的數值和或是最小值，如果是靜態資料，也就是陣列內容不會再改變，我們可以用 prefix sum 在 constant time 取得結果
但如果陣列的值會改變，就需要每次都重新計算 prefix sum，此時的時間複雜度會是 O(N)，有沒有更快的方法呢？
這邊有兩個相似的樹狀結構 Segment Tree / Binary Indexed Tree (又稱 Fenwick Tree) 可以用 O(logN) 解決動態區間和的問題，其中 Segment Tree 可以更廣泛解決區間極值的問題
相關題目
- 307. Range Sum Query - Mutable
- 308. Range Sum Query 2D - Mutable
- 315. Count of Smaller Numbers After Self
- 327. Count of Range Sum
Segment Tree
教學影片：Segment Tree Data Structure - Min Max Queries
Segment Tree 與 BIT 的概念雷同，原本我用 prefix sum 遇到更新時要用 O(n) 整個重建，但如果我把區間切小，每次更新只要影響到部分區間，對應的讀取要篩選符合的區間讀取，妥協後 讀取與更新都控制在 log(N)，但區間該怎麼切以及如何實作呢？ 這就是 Segment Tree 與 BIT 不同之處
Segment Tree 用陣列儲存區間值，需要兩倍額外記憶體空間，原陣列放在新陣列的最後，接著往前跟新區間 (parent = idx/2)，如下圖 (從影片截圖而來)
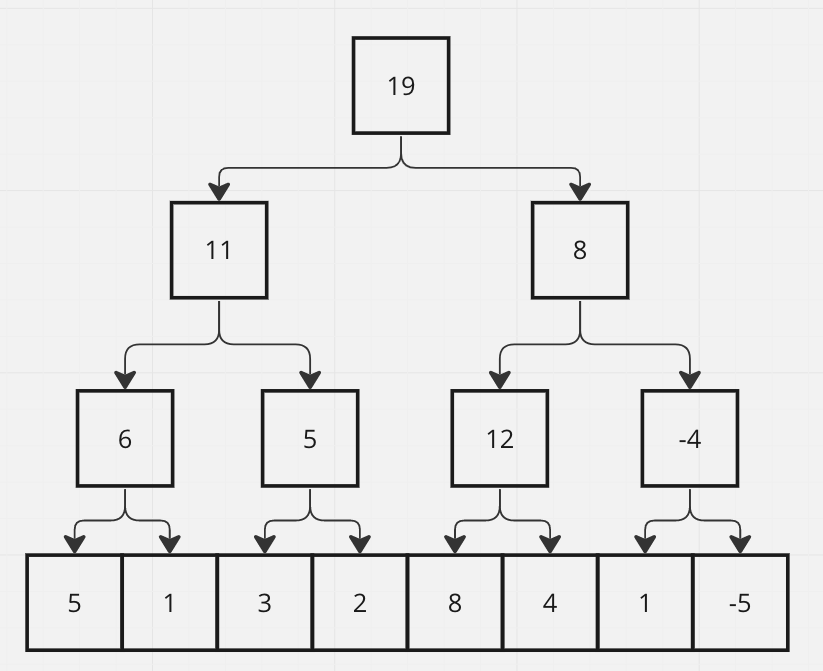
所以區間是 2 -> 4 -> 8 這樣往上疊加
初始化程式碼為
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| class SegmentTree {
public:
SegmentTree(const std::vector<int>& nums) {
offset_ = nums.size();
nodes_.resize(offset_ * 2, 0);
// 先把原陣列放在最後
for (int i = 0; i < offset_; i++) {
nodes_[i + offset_] = nums[i];
}
// parent = 左 child + 右 child
for (int i = offset_ - 1; i > 0; i--) {
nodes_[i] = nodes_[i * 2] + nodes_[i * 2 + 1];
}
}
void update(int index, int val) {
// 因為有移動，所以要加上 offset_
int nodeIdx = index + offset_;
int diff = val - nodes_[nodeIdx];
// 更新時要更新全部的 parent
while (nodeIdx > 0) {
nodes_[nodeIdx] += diff;
nodeIdx /= 2;
}
}
private:
int offset_;
std::vector<int> nodes_;
};
|
透過 O(N) 即可完成初始化，我們將原陣列放在最後，並往上疊加出多個區間，Update 需要 O(logN)，因為要往前把相關的區間都要更新一次
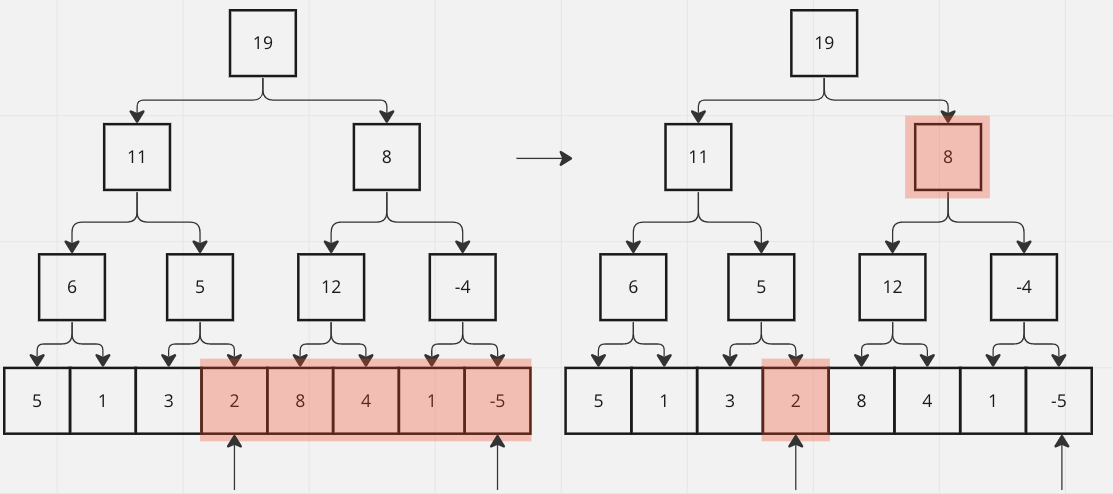
接著重點是 range query，傳入 left / right (閉區間) 要在 O(logN) 解決，重點，
- 如果我們查找的範圍會涵蓋完整區間，往上找區間值
- 反之，則取得當下的值，並往下一個區間邁進
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| int sumRange(int left, int right) {
int nodeLeftIndex = left + offset_;
int nodeRightIndex = right + offset_;
int count = 0;
while (nodeLeftIndex <= nodeRightIndex) {
// 如果是左指針，且指到區間右側，當下取值
if ((nodeLeftIndex & 1) == 1) {
count += nodes_[nodeLeftIndex];
nodeLeftIndex++;
}
// 如果是右指針，且指到區間左側，當下取值
if ((nodeRightIndex & 1) == 0) {
count += nodes_[nodeRightIndex];
nodeRightIndex--;
}
nodeLeftIndex /= 2;
nodeRightIndex /= 2;
}
return count;
}
|
如果想要查詢整段區間的指標移動，我們可以觀察出一個重點
偶數 index 都在區間的左側 / 奇數 index 是在區間的右側
因為我們是用 left / right 去找區間和，所以我們要找left 往右找與 right 往左找的共同區間，總共分成 4 種情況考慮
- left 指向偶數：
代表我們會拿整個區間，因為區間的左側是偶數，當目前 left 就指向偶數，代表要取出整個區間 - left 指向奇數：
代表我們不可以拿區間當作代表，因為奇數是區間的右側，再往下就到另一個區間，所以我們要直接取值 - right 指向偶數：
right 跟 left 邏輯剛好相反，我們只能拿 right 往左的區間，因為偶數是 parent 左側，再往下移就到下個區間，所以要拿當前值 - right 指向奇數：
因為奇數是區間的右側，代表我們可以拿整個區間為當前值
以上圖為例
- 左指針指向 -2，此時是區間的右側，符合條件 2，拿完 -2 往下一個區間走 / 右指針只在區間右側符合條件4，往上一個區間
- 左指針持續指向區間左側符合條件1、右指針指向區間右側符合條件4，一路往上指到同一個區塊，直接拿完整段區間 (8~-5)
影片參考資料是左閉右開的計算方式，但這樣我覺得再取出區間和比較不好做，所以參考 leetcode 解答調整成目前的閉區間算法
307. Range Sum Query - Mutable 完整解法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
| class SegmentTree {
public:
SegmentTree(const std::vector<int>& nums) {
offset_ = nums.size();
nodes_.resize(offset_ * 2, 0);
for (int i = 0; i < offset_; i++) {
nodes_[i + offset_] = nums[i];
}
for (int i = offset_ - 1; i > 0; i--) {
nodes_[i] = nodes_[i * 2] + nodes_[i * 2 + 1];
}
}
void update(int index, int val) {
int nodeIdx = index + offset_;
int diff = val - nodes_[nodeIdx];
while (nodeIdx > 0) {
nodes_[nodeIdx] += diff;
nodeIdx /= 2;
}
}
int sumRange(int left, int right) {
int nodeLeftIndex = left + offset_;
int nodeRightIndex = right + offset_;
int count = 0;
while (nodeLeftIndex <= nodeRightIndex) {
if ((nodeLeftIndex & 1) == 1) {
count += nodes_[nodeLeftIndex];
nodeLeftIndex++;
}
if ((nodeRightIndex & 1) == 0) {
count += nodes_[nodeRightIndex];
nodeRightIndex--;
}
nodeLeftIndex /= 2;
nodeRightIndex /= 2;
}
return count;
}
private:
int offset_;
std::vector<int> nodes_;
};
class NumArray {
public:
NumArray(vector<int>& nums) {
tree_ = new SegmentTree(nums);
}
void update(int index, int val) {
tree_->update(index, val);
}
int sumRange(int left, int right) {
return tree_->sumRange(left, right);
}
private:
SegmentTree* tree_;
};
/**
* Your NumArray object will be instantiated and called as such:
* NumArray* obj = new NumArray(nums);
* obj->update(index,val);
* int param_2 = obj->sumRange(left,right);
*/
|
Binary Index Tree
1994 年的論文 A New Data Structure for Cumulative
Frequency Tables / 我覺得講得很好的影片 Fenwick Tree (Binary Index Tree) - Quick Tutorial and Source Code Explanation
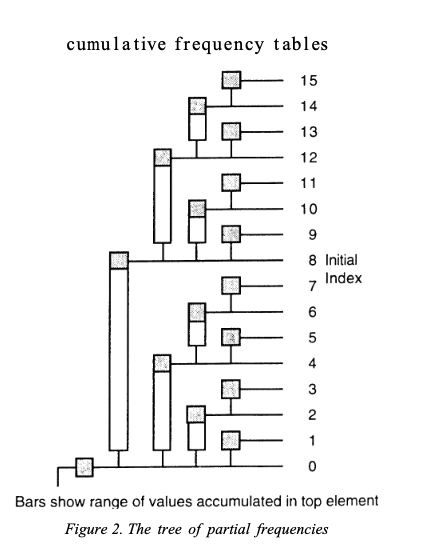這張圖是從論文截圖而來，實作技巧非常巧妙，他利用 Last Significant Bit (LSB) 來決定區間的範圍，如果 LSB 是 xxx1，則只儲存當前一個數，如果 LSB 是 xx10，則儲存當前兩個數，以此類推，所以可以看到 1, 3 等只會儲存當前 1 個數、8 會儲存往前 8 個數
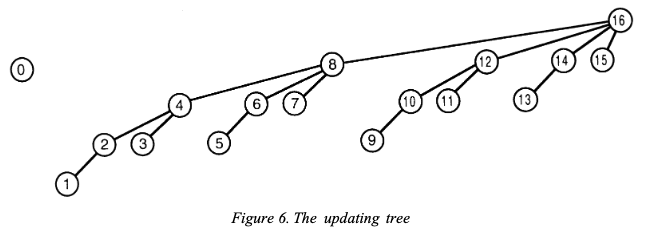所以更新時會需要更新所有相關區間，上面這張圖是代表當你更新 index i 時，需要往上調整的 bit index，例如更新 idx 1 時，因為 bit[2]、bit[4]、bit[8] 都有包含 idx 1，所以都要一併更新
實作方面非常簡單，透過 2 補數 i & -i 即可取得 LSB
1
2
3
4
5
6
7
8
9
| // 1: 0001
//-1: 1111
// 1 & -1 => 0001
// 6: 0110
//-6: 1010
// 6 & -6 => 0010
int getParent(int i) {
return i + (i & -i);
}
|
讓我們看查詢會變得如何：
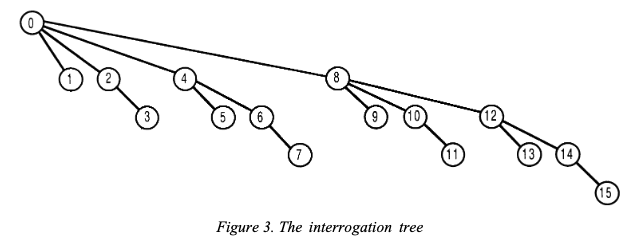圖片表達如果你要某個 prefix sum，你必須往前輪詢的 index，例如要找 idx 1~9 的 prefix sum，則需要 bit[9] + bit[8]，搭配上一張圖 bit[9] 只有儲存 idx 9 這個元素，而 bit[8] 儲存了 idx 1-8 個元素
實作方面同樣透過 2 補數，只是變成往下減
1
2
3
| int getNextInterval(int i) {
return i - (i & -i);
}
|
整體實作
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
| class BIT {
public:
BIT(const std::vector<int>& nums) {
int size = nums.size();
// index 從 1 開始比較好計算
bit_.resize(size + 1, 0);
arr_.resize(size, 0);
// 初始化只要往下一個 parent 加
// 後面 iterate 會疊上去
for (int i = 0; i < size; i++) {
int bitIdx = i + 1;
bit_[bitIdx] += nums[i];
arr_[i] = nums[i];
int parent = getParent(bitIdx);
if (parent < bit_.size()) {
bit_[parent] += bit_[bitIdx];
}
}
}
void update(int index, int val) {
int diff = val - arr_[index];
arr_[index] = val;
index++;
// 更新記得要全部包含的區間都更新
while (index < bit_.size()) {
bit_[index] += diff;
index = getParent(index);
}
}
int prefixSum(int index) {
int count = 0;
index++;
// 取值要往前推
while (index > 0) {
count += bit_[index];
index = getNextInterval(index);
}
return count;
}
private:
std::vector<int> bit_;
std::vector<int> arr_;
int getParent(int i) {
return i + (i & -i);
}
int getNextInterval(int i) {
return i - (i & -i);
}
};
class NumArray {
public:
NumArray(vector<int>& nums) {
tree_ = new BIT(nums);
}
void update(int index, int val) {
tree_->update(index, val);
}
int sumRange(int left, int right) {
return tree_->prefixSum(right) - tree_->prefixSum(left - 1);
}
private:
BIT* tree_;
};
|
小結：BIT vs Segment Tree
整理一下兩者
| 比較 | | |
|---|
| 操作 | Segment Tree | Binary Index Tree |
| 記憶體空間 | 2 * n | n |
| 初始化 | O(n) | O(n) |
| 查詢 | O(logN) | O(logN) |
| 更新 | O(logN) | O(logN) |
此外，使用上兩者有共同侷限 新增 / 移除元素需要重新初始化
兩者差異
兩者都可以解決 #307 這道題目，但看似相同但還是有差異之處，簡單來說 Segment Tree 用途更廣，BIT 只能解決 Prefix Sum 計算
例如 Segment Tree 還可以解決區間最小值/區間最大值，而 BIT 是做不到的，為什麼？
因為 BIT 並不是儲存每一個值，而是在初始化就以區間的形式保存，如果是加法這種 invertible 算法，意即我區間儲存 (a+b), 我可以透過 (a+b) - a 還原 b 的值；
但求極值是 non invertable，如果要用 BIT 求極值，那麼在區間計算時就用儲存極值，這樣更新時就會出錯
1
2
3
4
5
| 原陣列：[3, 2]
BIT: [, 3, 3(保存區間極值)]
update (0, 1)
BIT: [, 1, ?] => 無法計算
|
所以 BIT 用途比較侷限，但優點是記憶體空間小，而且 bitwise 的計算速度會快更多
有一篇論文寫可以用兩個 BIT 實作區間極值的查詢，結果還是比 Segment Tree 快上許多，可以參考看看 Efficient Range Minimum Queries - using Binary Indexed Trees